B2 - MAOL

MATEMATIIKKA B2

Tehtävänanto

”Leena haluaa tutkia kolmannen asteen polynomeja. Hän muodostaa polynomin [[$$ax^3+bx^2+cx+d$$]] kertoimet [[$a$]], [[$b$]], [[$c$]] ja [[$d$]] heittämällä noppaa. Millä todennäköisyydellä hänen polynominsa on kasvava? Jos hän muodostaa samalla tavalla 5 polynomia, niin millä todennäköisyydellä mikään niistä ei ole kasvava? Voit käyttää tilanteen hahmottamisen apuna alla olevaa Geogebra-esimerkkiä, mutta pelkkä kokeilu ei riitä perusteluksi.”

(lähde: https://digabi.fi/kokeet/esimerkkitehtavat/matematiikka/matematiikan-esimerkkitehtava-b-osa/)
Luettu 1.9.2017

B2 – YTL ja Calc

Näyttökuva 2018-03-17 kello 9.40.00.png

Näyttökuva 2017-10-08 kello 19.54.33.png

Näyttökuva 2018-03-17 kello 9.40.46.png

B2 – Casio

B2 – GeoGebra

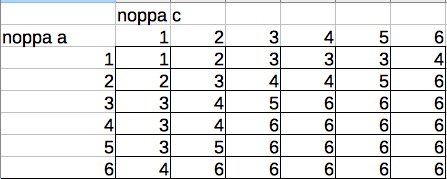
Polynomifunktio f on kasvava, kun derivaatta on suurempaa tai yhtä suurta kuin nolla kaikilla muuttujan x arvoilla.

Näyttökuva 2017-08-26 kello 21.06.23.png

Kertoimet arvotaan nopalla, joten a > 0 ja derivaattafunktion kuvaaja on ylöspäin aukeava paraabeli. Derivaatta on suurempaa tai yhtä suurta kuin nolla eli $f'ge0$ , kun derivaattafunktiolla on korkeintaan yksi nollakohta.

Näyttökuva 2017-08-26 kello 21.08.29.png

Derivaatta on 2. asteen polynomifunktio, joten sillä on korkeintaan yksi nollakohta kun diskriminantti on pienempää tai yhtä suuri kuin nolla. Kertoimet a, b ja c arvotaan nopalla. Tehdään 6 x 6 ruudukko, johon merkitään suotuisien alkeistapauksien lukumäärä.

Näyttökuva 2017-08-26 kello 21.16.51.png

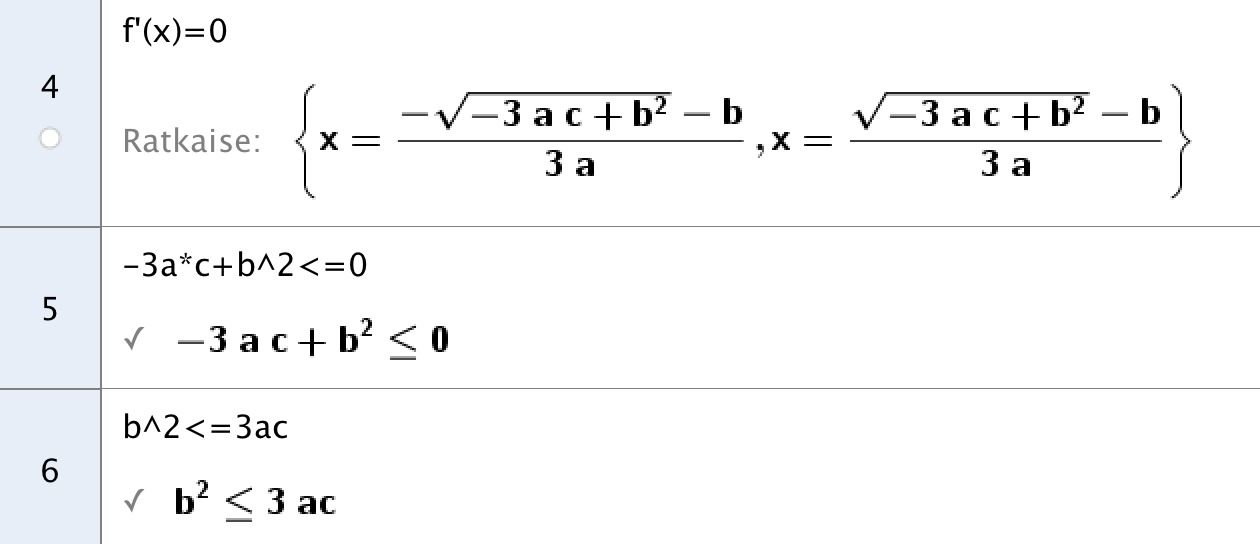
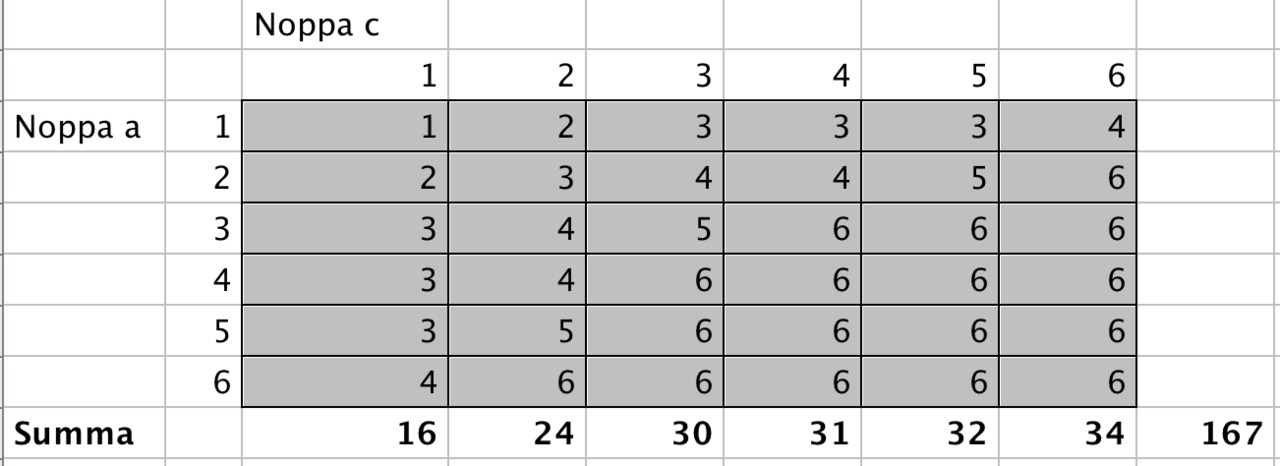Suotuisia alkeistapauksia on yhteensä 167 ja kaikki alkeistapaukset kolmen nopan heitossa ovat

$6^3=216.$ Todennäköisyys, että funktio $f$ on kasvava on

$Pleft(f mathrmright)=frac=0,773... approx0,77$

Vastaus: 77% todennäköisyydellä

Geogebralla hieman toisella tavalla

Alku, kuten yllä. Tutkitaan diskriminanttia.
Voidaan luoda taulukot, joissa arvoina on diskriminantin arvot.

Saadaan kuusi kappaletta 6*6 taulukkoa, joista kaksi yläpuolella ja loput neljä alapuolella.

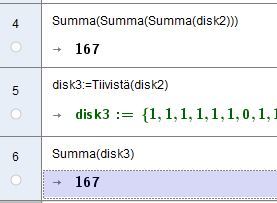
Oikeastaan meitä ei kiinnosta diskrimininanttien arvot, vaan onko D<=0. Samankaltaisella komennolla saadaan ne valittua.
Kolminkertaisen jono-komennon sisällä on jos-komento jos( diskriminantti >=0, niin arvo on 1, muuten arvo on nolla)

disk2:=Jono(Jono(Jono(Jos((2*b)^2-4*3*a*c

Koska taulukoissa on kolme sisäkkäistä taulukkoa, yllä olevista ykkösistä saadaan summa kolmella summa komenonlla. Vaihtoehtoisesti Tiivistä-komennolla saadaan lista ”samaan tasoon”, niin yksi summa komento riittää.

B2 – TI-Nspire

Samalla idealla olisi voinut tehdä GeoGebralla tai Casiolla. Geogebran jono-komento olisi tässä kohtaa hyödyllinen.

TAPA2
Laitetaan taulukkoon luvut 1…216 ja tuotetaan viereen lukujen a,b ja c arvot sekä omaan sarakkeeseen diskriminantin arvo, josta lasketaan suotuisat alkeistapahtumat.

Ratkaisutiedostot

Lataa tiedostot zip-pakettina tästä

Tunnistaudu

Etkö ole vielä jäsen?

MATEMATIIKKA B2

B2 – YTL ja Calc

B2 – Casio

B2 – GeoGebra

B2 – GeoGebra

B2 – TI-Nspire

Ratkaisutiedostot