En horisontell cylindertank

Exempel räkna volymen om höjden är 75%

Skärmbild från 2018-02-27 10-12-19.png

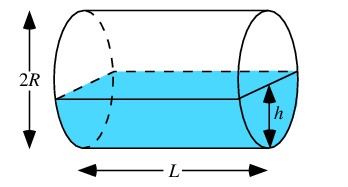
Uppgift

En liggande rak cylinderformad tank rymmer 5000 liter.
Tanken har längden L=4,00 m.

Bestäm

a) den cirkelformade sidans area

b) höjden eller sidans diameter

c) volymen som återstår att fylla då tanken
fyllts till 75% av höjden.

d) Här är mätvärden

höjd /radie	relativ volym /full tank
0.0	0.0
0.1	0.0186930367342493
0.2	0.0520440193309140
0.3	0.0940602021870938
0.4	0.142378489932647
0.5	0.195501109477886
0.6	0.252315787734346
0.7	0.311918832390537
0.8	0.373530039052331
0.9	0.436444285784770
1.0	0.500000000000000
1.1	0.563555714215232
1.2	0.626469960947670
1.3	0.688081167609464
1.4	0.747684212265655
1.5	0.804498890522116
1.6	0.857621510067354
1.7	0.905939797812907
1.8	0.947955980669087
1.9	0.981306963265752
2.0	1.0

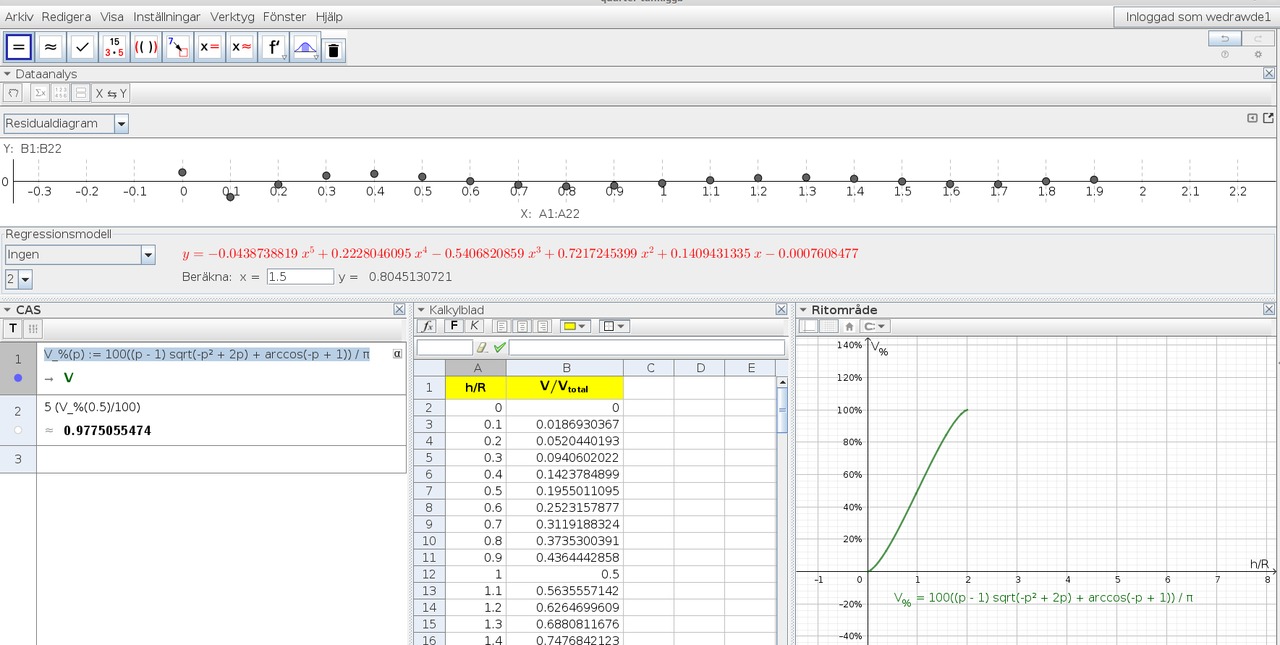
Pröva att anpassa ett 5-gradspolynom.

Härled en funktion som tar in p=procent av radien som uppnåtts p=0..2 och ger volymprocent.

Lösning:
Skärmbild från 2018-02-26 23-12-12.png

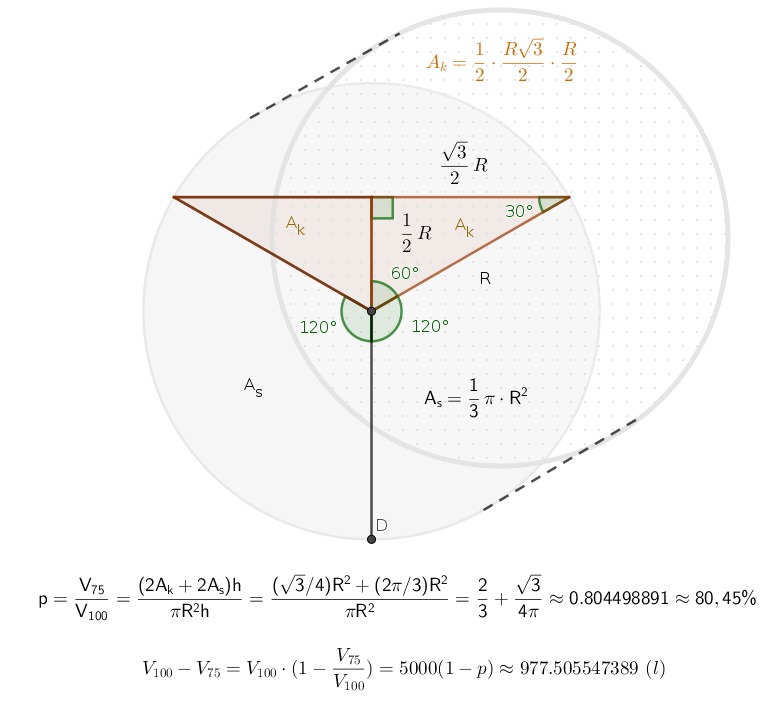
=\frac{V_{75}}{V_{100}}=\frac{(2A_k+2A_s)h}{\pi R^2h}=\frac{(\sqrt{3}/4)R^2+(2\pi/3) R^2}{\pi R^2}=\frac{2}{3}+\frac{\sqrt{3}}{4\pi}\approx 0.804498891 \approx 80,45\%

V_{100}-V_{75}=V_{100}\cdot(1-\frac{V_{75}}{V_{100}})=5000(1-p)\approx 977.505547389\,\, (l)

Arean av triangeln i en cirkelsektor med vinkeln α
$A_=frac(Rsinfrac{alpha})(Rcosfrac{alpha})=fracR^2sinalpha$

A_{triangel}=\frac{1}{2}(R\sin\frac{\alpha}{2})(R\cos\frac{\alpha}{2})=\frac{1}{2}R^2\sin\alpha

och arean av cirkelsektorn
$A_=frac{alpha}pi R^2=frac{alpha}R^2$

A_{sektor}=\frac{\alpha}{2\pi}\pi R^2=\frac{\alpha}{2}R^2

Cirkelsegment är skillnaden
$A_=frac{alpha}R^2-fracR^2sinalpha=fracR^2left(alpha-sinalpharight)$

A_{segment}=\frac{\alpha}{2}R^2-\frac{1}{2}R^2\sin\alpha=\frac{1}{2}R^2\left(\alpha-\sin\alpha\right)

Vi mäter höjden från andra ändan.
$cosfrac{alpha}=frac=1-frac$
$sinfrac{alpha}=sqrtright)^2}=sqrt{frac-frac}=fraccdotsqrt$

\cos\frac{\alpha}{2}=\frac{R-h}{R}=1-\frac{h}{R} \sin\frac{\alpha}{2}=\sqrt{1-\left(\frac{R-h}{R}\right)^2}
=\sqrt{\frac{2h}{R}-\frac{h^2}{R^2}}=\frac{1}{R}\cdot\sqrt{2Rh-h^2}

Insättning och formeln
$sinalpha = 2sinfrac{alpha}cosfrac{alpha}$

\sin\alpha\ =\ 2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}

ger

$A=R^2cdotcos^{-1}left(fracright)-left(R-hright)sqrt$
vi substituerar
$h=pR$
⇒
$A=R^2cdotleft(cos^{-1}left(1-pright)-left(1-pright)sqrtright)$

A=R^2\cdot\left(\cos^{-1}\left(1-p\right)-\left(1-p\right)\sqrt{2p-p^2}\right)

$V_{%}left(pright)=100cdotfrac{pi R^2L}=100cdotfrac}{pi R^2}=frac{cos^{-1}left(1-pright)-left(1-pright)sqrt}{pi}$

V_{\%}\left(p\right)=100\cdot\frac{V}{\pi R^2L}=100\cdot\frac{A_{ }}{\pi R^2}
=\frac{\cos^{-1}\left(1-p\right)-\left(1-p\right)\sqrt{2p-p^2}}{\pi}

Skärmbild från 2018-02-27 13-15-04.png
Litet analys med Geogebra.

Skärmbild från 2018-02-27 12-21-21.png

Geometriexempel

Ratkaise lieriönmuotoisen astian kokonaistilavuudesta puuttuva osa kun astian vedenpinnan korkeus on 0.75%.

Lasketaan kyljellään olevan lieriön päädyssä olevien ympyröiden alat. Tilavuus on V = 5000 litraa = 5 m³.

Leveys/korkeus h=4 m. Suoran lieriön pinta-ala A = V/h = 5/4 = 1,25 (m²). Pääty-ympyröiden mitat

$r=sqrt{frac{pi}}=fracsqrt{frac{pi}}approx0.6307831305 left(mright)$

r=\sqrt{\frac{A}{\pi}}=\frac{1}{2}\sqrt{\frac{5}{\pi}}\approx0.6307831305\

$d=2r=sqrt{frac{pi}}approx1.26156626101 left(mright)$

d=2r=\sqrt{\frac{5}{\pi}}\approx1.26156626101\ \left(m\right)

$p=pi d=sqrt$

p=\pi d=\sqrt{5\pi}

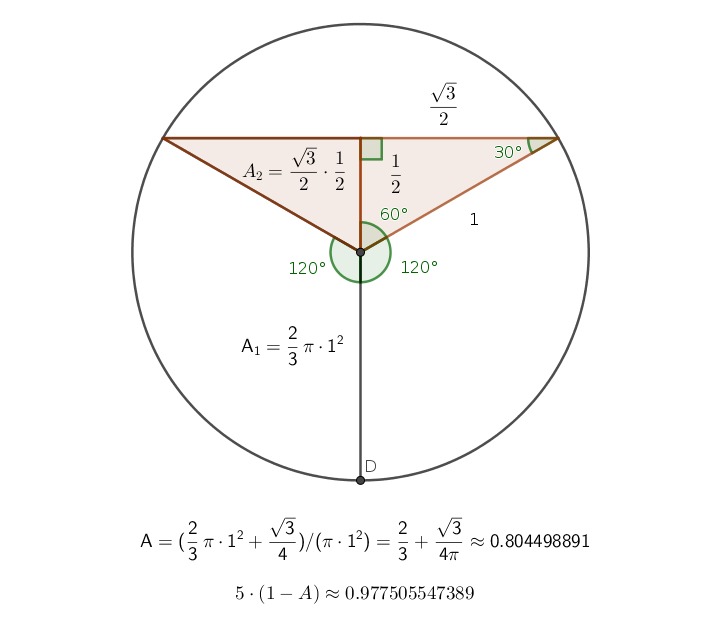
Lasketaan tilavuus kun pinta on 75% kohdalla. Sektoreiden kulmat

$sinalpha=frac{frac}=fracRightarrowalpha=30°$

\sin\alpha=\frac{\frac{r}{2}}{r}=\frac{1}{2}\Rightarrow\alpha=30°

Sektorien ala 2 kpl:
$A_2=fraccdot A=frac approx0.20833333333 left(m^2right)$

A_2=\frac{60°}{360°}\cdot A=\frac{A}{6}\ \approx0.20833333333\ \left(m^2\right)

Kolmioiden pinta-ala

$A_3=left(fracrright)cdotsqrtrright)^2}=r^2cdotfrac{sqrt}=frac}{picdot4}=frac}approx2cdot0.17229027981 left(m^2right)$

_3=\left(\frac{1}{2}r\right)\cdot\sqrt{r^2-\left(\frac{1}{2}r\right)^2}=r^2\cdot\frac{\sqrt{3}}{4}=\frac{A\cdot\sqrt{3}}{\pi\cdot4}=\frac{5\cdot\sqrt{3}}{16\cdot\pi}\approx2\cdot0.17229027981\ \left(m^2\right)

$V_0=V-Vleft(frac+frac+frac{sqrt}right)=5left(frac-frac{sqrt}right)=frac}approx0.97750554738 left(m^3right)$

V_0=V-V\left(\frac{1}{2}+\frac{1}{6}+\frac{\sqrt{3}}{4\pi}\right)=5\left(\frac{1}{3}-\frac{\sqrt{3}}{4\pi}\right)=\frac{20-3\sqrt{3}}{12\pi}\approx0.97750554738\ \left(m^3\right)

Tunnistaudu

Etkö ole vielä jäsen?

Exempel räkna volymen om höjden är 75%

Geometriexempel