Suora koostuu pisteistä, joita on äärettömän tiheässä. Suoralla ei ole päätepisteitä, mutta jos tasoon merkitään kaksi pistettä, niiden kautta voidaan piirtää suora. Näin voidaan toimia myös koordinaatistossa; jos koordinaatistosta valitaan kaksi pistettä, niiden kautta voidaan piirtää suora. Samaiselta suoralta voidaan tarkastella mitä tahansa pistettä, ja erityisesti sen koordinaatteja. Ei ole sattumanvaraista, miten suoran pisteen x- ja y- koordinaatit suhtautuvat toisiinsa. Ohessa esimerkki 1, jossa suoralta on valittu muutama piste, ja pisteiden x- ja y- koordinaatit on merkitty taulukkoon.
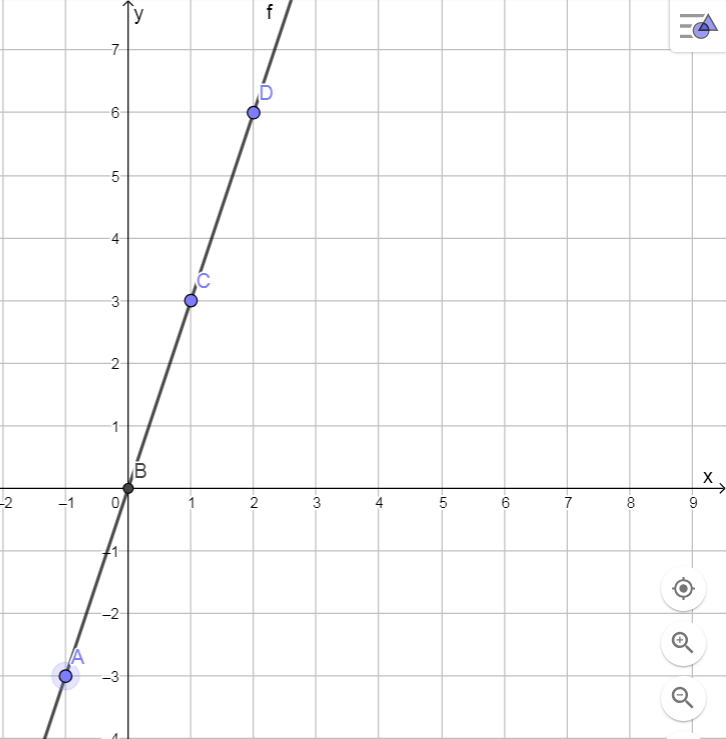
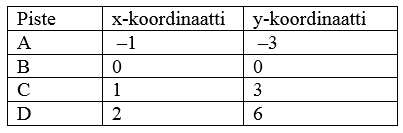
Taulukon avulla huomataan, että y-koordinaatti on aina kolminkertainen x-koordinaattiin nähden. X:n ja y:n välillä on matemaattinen yhteys; jokaiselle suoran pisteelle voidaan todeta että y = 3·x eli lyhemmin y = 3x. Tätä matemaattista yhteyttä kutsutaan suoran yhtälöksi.
Esimerkki 2:
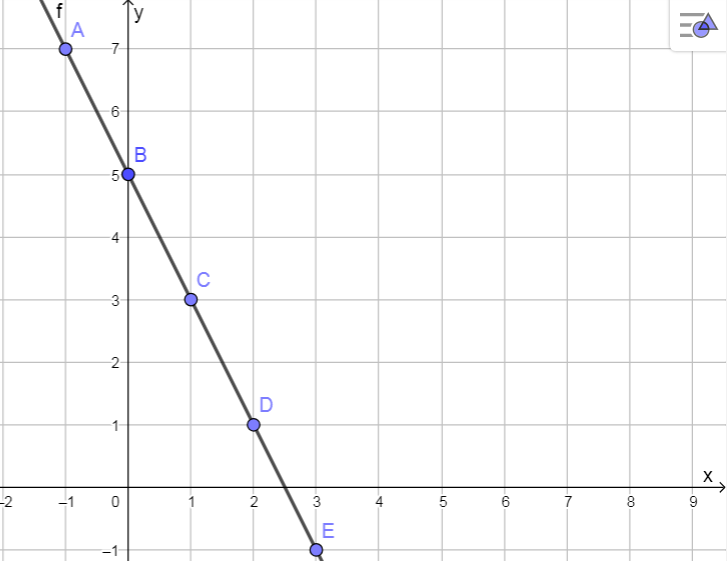
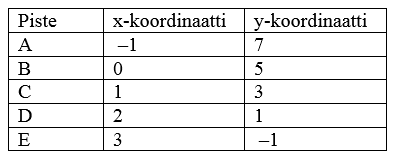
Tässä kuvassa on toinen suora, ja siltä valitut viisi pistettä. Nytkin huomataan, että x:n ja y:n välillä on olemassa matemaattinen yhteys; y-koordinaatti saadaan, kun x-koordinaatti kerrotaan –2:lla ja tuloon lisätään luku 5. Suoran yhtälö on siten y = –2x + 5.
Mikäli suoran yhtälö tunnetaan, voidaan suora piirtää koordinaatistoon itse. X-koordinaatin arvo voidaan valita itse, ja suoran yhtälön avulla lasketaan y-koordinaatin arvo. Suoran piirtämiseksi riittäisi, kun laskettaisiin kaksi pistettä, mutta kolmas piste on hyvä laskea varmuuden vuoksi. Koordinaattilaskut voidaan esittää selkeästi taulukossa.
Esimerkki 3. Olkoon jokin suoran yhtälö y = 2x – 4. X-koordinaateiksi voidaan valita vaikkapa 0, 1 ja 2. Oheisessa taulukossa on laskettu y –koordinaattien arvo, ja viimeiseen sarakkeeseen on merkitty pisteiden koordinaatit.
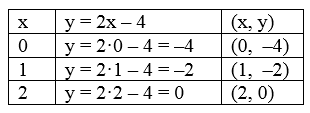
Koordinaattipisteet voidaan merkitä koordinaatistoon, ja piirtää suora niiden avulla:
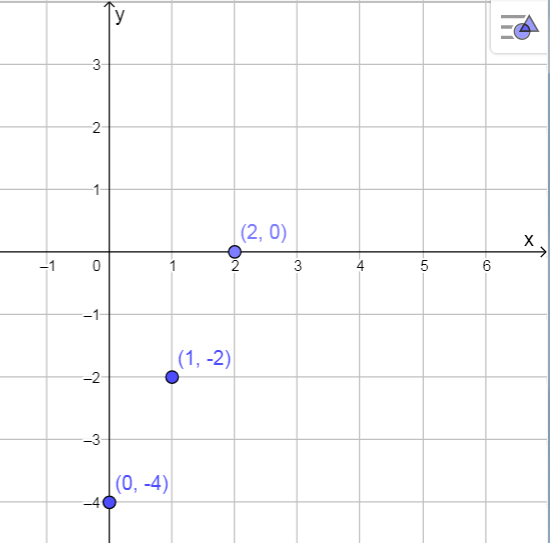
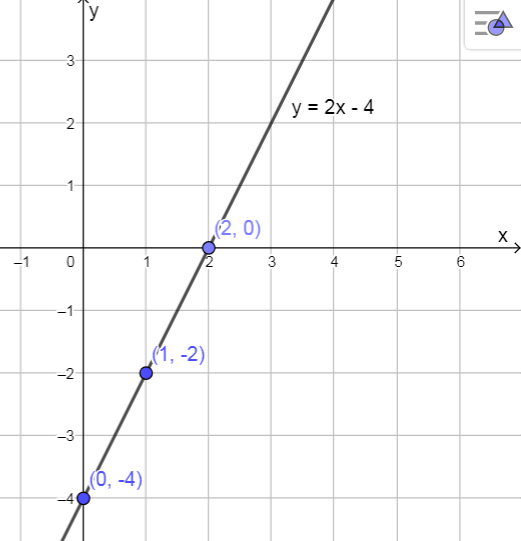
Suoran piirtämistä on syytä harjoitella ensin käsin paperille, ja kokeilla vasta sen jälkeen piirtämistä Pythonilla.
Suoraan liittyviä ohjelmointiharjoituksia on seuraavissa kappaleissa.


